Our selection of the top business news sources on the web.

AM edition. Issue number 1047

Latest 10 stories. Click the button for more.

Quote: William F. Sharpe - Nobel Laureate in Economics

“Question not only everybody else’s work, but question your own work as you do it, let alone after it’s done.” - William F. Sharpe - Nobel Laureate in Economics

William F. Sharpe’s advice—to “question not only everybody else’s work, but question your own work as you do it, let alone after it’s done”—reflects the relentless intellectual self-scrutiny that has defined his career and shaped the field of financial economics. Sharpe delivered this insight in a 2004 Nobel Prize interview, recalling how the discipline of constant self-questioning was instilled in him by his mentor Armen Alchian at UCLA. The ethic to act as one’s own toughest reviewer permeated Sharpe’s approach to research and innovation, driving his work to the highest standards of analytical rigour throughout a career that upended how global markets understand risk and return.

Sharpe’s journey began in Boston in 1934 and traversed the turbulence of war-era America, eventually landing him at UCLA, where changing his studies from medicine to economics would alter the trajectory of his life. Inspired by Alchian’s rigour and by J. Fred Weston’s introduction to the still-nascent field of portfolio theory, Sharpe was quickly drawn to the beauty of mathematical logic applied to real-world economic problems. He honed his analytical skill during years of study and early research at RAND Corporation, where he encountered Harry Markowitz, whose pioneering work on portfolio selection laid the groundwork for Sharpe’s own breakthroughs.

It was Sharpe's drive to question assumptions and his openness to self-critique that enabled him to distil Markowitz’s complex mean-variance model into the elegant Capital Asset Pricing Model (CAPM). This model became the backbone of modern finance, fundamentally altering how the risk and return of risky assets are priced and giving birth to the now ubiquitous concept of “beta.” Published in 1964 after initial scepticism from academic gatekeepers, Sharpe’s work, completed in parallel with Jack Treynor, John Lintner, and Jan Mossin, revolutionised both theory and practice. The CAPM forms the intellectual infrastructure for everything from index fund investing to performance benchmarking, nurturing a global culture in which prudent risk-taking is measurable, comparable, and improvable. Sharpe’s subsequent innovations, including the Sharpe Ratio, reinforced his belief that rigorous, repeatable self-examination is essential for practical financial decision-making as well as academic advancement.

Sharpe’s career is remarkable not just for his theoretical contributions, but for his insistence on connecting model with reality. He split his time between academia (with appointments at the University of Washington, Stanford, and elsewhere) and hands-on consulting, founding Sharpe-Russell Research to advise some of the world’s largest investors and co-founding Financial Engines, an early pioneer in digital investment advice. Throughout, he has focused on making abstract models relevant for individual and institutional investors, and on adapting theory to the rapidly evolving realities of global capital markets. His Nobel Prize in 1990, shared with Markowitz and Merton Miller, formalised his status as a founder of modern financial economics.

The backstory of Sharpe’s impact is inseparable from the broader evolution of risk and investment theory in the twentieth century. Harry Markowitz, often considered the father of modern portfolio theory, provided the first quantitative framework for balancing risk and return through diversification. Markowitz’s work enabled rigorous measurement of portfolio variance and set the stage for Sharpe’s insight that only systematic, market-related risk is priced in rational markets. Merton Miller, the other co-recipient of the 1990 Nobel, contributed critical insights into corporate finance, market efficiency, and capital structure, further solidifying the empirical and analytical basis for much of today’s investment practice.

Sharpe’s quote, therefore, encapsulates the ethos of the scientific method as it applies to finance: progress is made not through mere acceptance or simple iteration, but through persistent, honest, and sometimes uncomfortable dialogue with one’s own assumptions and results. This disposition has not only underpinned Sharpe’s seminal achievements—transforming how markets price risk, fostering the index fund revolution, and shaping the metrics by which investment success is measured—but also compelled subsequent generations of theorists and practitioners to perpetually test, critique, and refine the frameworks upon which the security of trillions of dollars depends.

Term: The Capital Asset Pricing Model (CAPM)

A Comprehensive Analysis of Risk, Return and Modern Portfolio Theory

The Capital Asset Pricing Model (CAPM) stands as one of the most influential theoretical frameworks in modern finance, fundamentally transforming how investors, analysts, and financial theorists understand the relationship between risk and expected returns. Developed simultaneously by four brilliant economists in the early 1960s—William Sharpe, Jack Treynor, John Lintner, and Jan Mossin—CAPM emerged from Harry Markowitz's ground-breaking work on Modern Portfolio Theory to provide a mathematically elegant solution to the age-old investment question: what return should investors expect for bearing a particular level of risk? This revolutionary model established that only systematic, non-diversifiable risk should command a risk premium in efficient markets, suggesting that investors can achieve optimal portfolio performance through broad diversification whilst earning returns commensurate with their risk tolerance. The model's profound impact on financial practice cannot be overstated, as it provided the theoretical foundation for index fund investing, influenced regulatory frameworks such as the Prudent Investor Rule, and continues to guide trillions of dollars in institutional investment decisions worldwide, despite ongoing academic debates about its empirical validity and restrictive assumptions.

Definition and Core Conceptual Framework

The Capital Asset Pricing Model represents a mathematical framework that describes the linear relationship between systematic risk and expected return for individual securities and portfolios in financial markets. At its essence, CAPM posits that the expected return of any risky asset can be calculated by adding a risk premium to the risk-free rate, where the risk premium is determined by the asset's sensitivity to market movements multiplied by the market risk premium. This elegantly simple insight revolutionised investment theory by providing a quantitative method for determining whether securities are fairly priced relative to their risk characteristics.

The model's foundational principle rests on the distinction between systematic risk, which affects the entire market and cannot be eliminated through diversification, and idiosyncratic risk, which is specific to individual securities and can be diversified away. CAPM argues that rational investors should only be compensated for bearing systematic risk, as idiosyncratic risks can be eliminated through proper portfolio construction. This insight led to the profound realisation that holding a diversified portfolio aligned with market weightings represents the optimal investment strategy for most investors, as it maximises expected returns for a given level of systematic risk exposure.

The mathematical expression of CAPM takes the form of a linear equation where the expected return of asset i equals the risk-free rate plus beta multiplied by the market risk premium. Beta, the model's central risk measure, quantifies how much an asset's returns tend to move in relation to overall market movements, with a beta of 1.0 indicating returns that move in perfect synchronisation with the market, values above 1.0 suggesting amplified market sensitivity, and values below 1.0 indicating more stable, less volatile performance characteristics.

The theoretical elegance of CAPM lies in its ability to reduce the complex portfolio selection problem identified by Markowitz into a simple, two-fund theorem. According to this principle, all rational investors should hold portfolios consisting of only two components: the risk-free asset and the market portfolio of risky assets, with individual risk preferences determining the specific allocation between these two elements. This insight dramatically simplified investment decision-making whilst providing a coherent framework for understanding how asset prices should be determined in efficient markets.

Historical Development and Evolution

The development of the Capital Asset Pricing Model represents one of the most remarkable examples of simultaneous scientific discovery in the history of economic thought, with four economists independently arriving at essentially identical conclusions during the early 1960s. This extraordinary convergence of intellectual effort emerged from the fertile ground prepared by Harry Markowitz's pioneering 1952 paper on portfolio selection, which had established the mathematical foundation for modern portfolio theory but left unresolved the practical challenge of determining appropriate expected returns for individual securities.

Harry Markowitz had fundamentally transformed investment analysis by introducing rigorous mathematical methods to portfolio construction, demonstrating that investors could reduce portfolio risk through diversification without necessarily sacrificing expected returns. His work established the efficient frontier concept, showing that optimal portfolios could be constructed to maximise expected return for any given level of risk. However, Markowitz's original formulation required investors to estimate expected returns, variances, and covariances for all securities under consideration—a computationally intensive process that seemed impractical for real-world application with large numbers of securities.

The stage was set for further innovation when Markowitz began collaborating with his graduate student William Sharpe at UCLA in the late 1950s. Sharpe, who had initially been disappointed to discover that financial practice relied on "rule of thumb" rather than rigorous theory, became determined to apply newly developed computer programs and mathematical models to quantify market processes. Working under Markowitz's informal guidance, Sharpe developed what would become his doctoral dissertation, exploring ways to simplify the portfolio selection problem through the introduction of a single-factor model that related individual security returns to a common market factor.

Simultaneously, Jack Treynor was grappling with similar questions from a practitioner's perspective at Arthur D. Little consulting firm. Having studied mathematics at Haverford College before earning an MBA from Harvard Business School, Treynor had become frustrated with the arbitrary nature of discount rate selection in corporate finance decisions. During a three-week summer vacation in 1958, working in a cottage in Evergreen, Colorado, Treynor produced 44 pages of mathematical notes addressing the relationship between risk and appropriate discount rates—work that would form the kernel of what became known as CAPM.

John Lintner at Harvard Business School approached the capital asset valuation problem from yet another angle, focusing on the corporate perspective of firms issuing securities rather than the individual investor's portfolio selection challenge. His work complemented the insights being developed by Sharpe and Treynor, though the various researchers remained largely unaware of each other's parallel efforts for several years. Jan Mossin, working independently in Norway, completed this quartet of simultaneous discoverers, contributing his own mathematical formulation of the asset pricing relationship.

The publication history of these seminal contributions reveals the initial scepticism that greeted this revolutionary theory. Sharpe's paper, submitted to the Journal of Finance in 1962, was initially rejected by referees who deemed its assumptions too restrictive and its results "uninteresting". Only after the journal changed editors was the paper finally published in 1964, ultimately becoming one of the most cited works in financial economics. Treynor's contribution faced an even more challenging publication path—his early draft circulated among the financial cognoscenti for decades before formal publication, earning him recognition as a foundational contributor despite the delayed formal acknowledgment.

Mathematical Foundation and Analytical Framework

The mathematical elegance of the Capital Asset Pricing Model lies in its ability to distil the complex relationship between risk and return into a single linear equation that captures the essential trade-offs facing investors in capital markets. The CAPM formula represents far more than a simple computational tool—it embodies a comprehensive theory of how rational investors should price risky assets in equilibrium:

The Capital Asset Pricing Model (CAPM) quantifies the link between an asset’s systematic risk and its expected return, proposing that investors require higher returns for taking on increased market risk.

Each component of the CAPM equation carries profound theoretical significance that extends well beyond its mathematical representation. The risk-free rate R_i serves as the foundational baseline return that investors can earn without bearing any uncertainty, typically proxied by government treasury securities due to their minimal default risk. This component acknowledges the time value of money principle, ensuring that all investment returns are evaluated relative to what could be earned from completely safe alternatives. The choice of appropriate risk-free rate proxy has evolved over time, with ten-year treasury yields becoming the standard benchmark for long-term investment analysis, though shorter-term rates may be more appropriate for specific applications.

Beta_i represents the model's central innovation, providing a standardised measure of systematic risk that captures how individual securities or portfolios respond to market-wide movements. Unlike traditional risk measures that focused on total volatility, beta isolates only that portion of risk that cannot be eliminated through diversification—the systematic risk that affects the entire market. Securities with betas greater than 1.0 exhibit amplified responses to market movements, experiencing larger gains during market upswings and steeper losses during downturns. Conversely, securities with betas below 1.0 demonstrate more stable performance characteristics, providing some insulation from market volatility whilst generally participating in market trends to a lesser degree.

The market risk premium (E(R_m) - R_f) represents the additional return that investors demand for bearing the uncertainty inherent in holding the overall market portfolio rather than risk-free securities. This component reflects the collective risk aversion of market participants and tends to fluctuate over time based on economic conditions, investor sentiment, and broader market dynamics. Historical estimates of the equity risk premium have varied considerably, with long-term averages typically ranging between 5-8% annually, though shorter-term variations can be substantially larger.

The linearity of the CAPM relationship embodies several profound theoretical implications that distinguish it from alternative asset pricing models. The linear form suggests that risk premiums increase proportionally with beta, meaning that an asset with twice the systematic risk should command twice the risk premium. This proportionality assumption has been subject to extensive empirical testing, with mixed results that have spawned numerous alternative models attempting to capture non-linear risk-return relationships.

Beta estimation itself represents a sophisticated econometric challenge that requires careful consideration of multiple factors including the choice of market proxy, measurement period, return frequency, and statistical methodology. Most practical applications calculate beta using ordinary least squares regression analysis, regressing individual asset returns against market returns over historical periods ranging from one to five years. However, the backward-looking nature of historical beta estimation raises important questions about its predictive validity, leading some practitioners to employ more sophisticated techniques such as adjusted beta calculations that account for the tendency of individual security betas to converge toward 1.0 over time.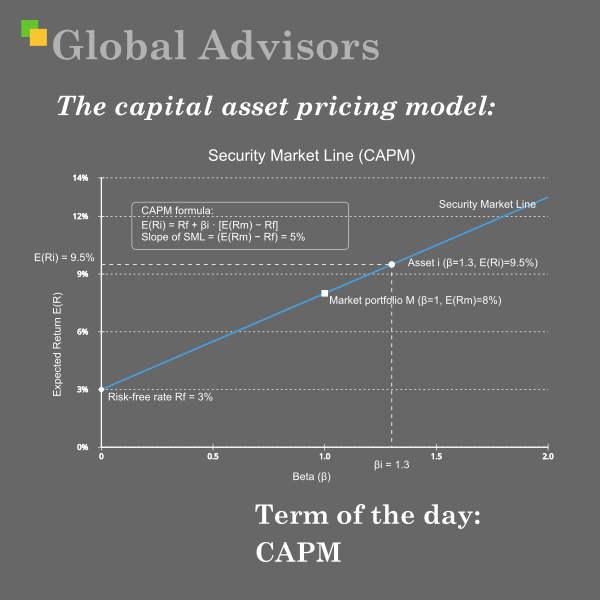

The graphic illustrates the Security Market Line (CAPM), plotting expected return against beta. The line intercepts the y-axis at the risk?free rate (3%), rises with a slope equal to the market risk premium (5%), and passes through the market portfolio at ? = 1 (8%). A sample asset at ? = 1.3 sits on the line at 9.5%, showing how CAPM links required return to systematic risk.

William Sharpe: The Primary Architect and Nobel Laureate

William Forsyth Sharpe emerges as the most prominent figure associated with the Capital Asset Pricing Model, not merely due to his Nobel Prize recognition in 1990, but because of his sustained contributions to financial theory and his role in bridging academic research with practical investment applications. Born on 16 June 1934 in Boston, Massachusetts, Sharpe's intellectual journey towards developing CAPM began during a peripatetic childhood shaped by his father's service in the National Guard during World War II. The family's eventual settlement in Riverside, California, provided the stable environment where young Sharpe's analytical talents could flourish, leading to his graduation from Riverside Polytechnic High School in 1951.

Sharpe's initial academic trajectory reflected the uncertainty typical of bright young students exploring their intellectual interests. Beginning his university education at UC Berkeley with intentions of pursuing medicine, he quickly discovered that his true passions lay elsewhere and transferred to UCLA to study business administration. However, even this focus proved insufficiently engaging, as Sharpe found accounting uninspiring and gravitated instead toward economics, where he encountered two professors who would profoundly influence his intellectual development: Armen Alchian, who became his mentor, and J. Fred Weston, who first introduced him to Harry Markowitz's revolutionary papers on portfolio theory.

The pivotal moment in Sharpe's career came through his association with the RAND Corporation, which he joined in 1956 immediately after graduation whilst simultaneously beginning doctoral studies at UCLA. This unique position at the intersection of academic research and practical problem-solving provided the ideal environment for developing the theoretical insights that would culminate in CAPM. At RAND, Sharpe encountered Harry Markowitz directly, leading to an informal but highly productive advisor-advisee relationship that would shape the trajectory of modern financial theory.

The intellectual genesis of CAPM can be traced to Sharpe's doctoral dissertation work in the early 1960s, where he grappled with the practical limitations of Markowitz's mean-variance optimisation framework. Whilst Markowitz had demonstrated the mathematical principles underlying efficient portfolio construction, the computational requirements of his approach seemed prohibitive for real-world application with large numbers of securities. Sharpe's breakthrough insight involved simplifying this complex optimisation problem through the introduction of a single-factor model that related individual security returns to a broad market index.

Sharpe's 1961 dissertation included an early version of what would become the security market line, demonstrating the linear relationship between expected return and systematic risk that forms the heart of CAPM. However, the path from academic insight to published theory proved challenging, as the financial economics establishment initially struggled to appreciate the revolutionary implications of this work. When Sharpe submitted his refined CAPM paper to the Journal of Finance in 1962, referees rejected it as uninteresting and overly restrictive in its assumptions. Only after the journal's editorial staff changed was the paper finally published in 1964, launching what would become one of the most influential theories in modern finance.

Following the publication of his seminal CAPM paper, Sharpe's career trajectory reflected his commitment to both theoretical development and practical application of financial insights. His move to the University of Washington in 1961 provided the academic platform for refining and extending his theoretical work, whilst his subsequent positions at UC Irvine and Stanford University established him as one of the leading figures in the emerging field of financial economics. Throughout this period, Sharpe continued to innovate, developing the Sharpe ratio for risk-adjusted performance analysis, contributing to options valuation methodology, and pioneering returns-based style analysis for investment fund evaluation.

Perhaps most significantly for the practical application of financial theory, Sharpe's work provided the intellectual foundation for the index fund revolution that transformed investment management. His demonstration that broad market diversification represented the optimal strategy for most investors directly supported the development of low-cost, passively managed investment vehicles that now manage trillions of dollars worldwide. This practical impact extended beyond portfolio management to influence regulatory frameworks, with Sharpe's insights contributing to the evolution of fiduciary standards and prudent investor guidelines.

The recognition of Sharpe's contributions culminated in his receipt of the 1990 Nobel Memorial Prize in Economic Sciences, shared with Harry Markowitz and Merton Miller, "for their pioneering work in the theory of financial economics". The Nobel Committee specifically recognised Sharpe's development of CAPM as providing the first coherent framework for understanding how risk should affect expected returns in capital markets. This recognition acknowledged not only the theoretical elegance of CAPM but also its profound practical implications for investment management, corporate finance, and financial regulation.

Sharpe's post-Nobel career demonstrated his continued commitment to bridging academic theory and practical application. His founding of Sharpe-Russell Research in 1986, in collaboration with the Frank Russell Company, focused on providing asset allocation research and consulting services to pension funds and foundations. This venture allowed Sharpe to implement the theoretical insights of CAPM and related models in real-world institutional investment contexts, demonstrating the practical value of rigorous financial theory whilst identifying areas where theoretical models required refinement or extension.

The intellectual legacy of William Sharpe extends far beyond the specific mathematical formulation of CAPM to encompass a broader vision of how financial markets should function and how investors should approach portfolio construction. His work established the theoretical foundation for understanding that diversification represents the only "free lunch" available to investors, whilst simultaneously demonstrating that attempts to outperform market benchmarks through security selection or market timing face significant theoretical and practical obstacles. These insights continue to influence investment philosophy and practice decades after their initial formulation, testament to the enduring value of Sharpe's contributions to financial understanding.

Applications and Practical Implementation

The practical applications of the Capital Asset Pricing Model extend far beyond academic theorising, fundamentally transforming how financial professionals approach investment valuation, portfolio construction, and risk management across diverse market contexts. The model's primary application lies in determining appropriate required rates of return for individual securities and portfolios, providing a systematic framework for evaluating whether investments are fairly priced relative to their risk characteristics. This capability has proven invaluable for investment analysts, corporate finance professionals, and institutional portfolio managers seeking objective methods for comparing investment opportunities.

In corporate finance applications, CAPM serves as the foundation for cost of equity calculations that drive fundamental valuation decisions including capital budgeting, merger and acquisition analysis, and strategic planning initiatives. Companies routinely employ CAPM-derived discount rates to evaluate potential investment projects, ensuring that capital allocation decisions reflect appropriate risk adjustments. The model's ability to provide standardised risk measures enables companies to compare projects across different business units and geographic regions, facilitating more informed strategic decision-making processes.

The implementation of CAPM in institutional investment management has perhaps generated the most significant practical impact, providing the theoretical justification for passive index investing strategies that now dominate large portions of global capital markets. Sharpe's insight that the market portfolio represents the optimal risky asset holding for most investors directly supported the development of broad-based index funds that seek to replicate market returns whilst minimising costs and tracking errors. This application has proven particularly influential in pension fund management, where fiduciary responsibilities require systematic approaches to risk management and return optimisation.

Portfolio managers utilise CAPM principles to construct efficient portfolios that balance risk and return considerations according to client preferences and constraints. The model's two-fund theorem suggests that optimal portfolio construction involves determining the appropriate allocation between risk-free assets and a diversified market portfolio, with individual risk tolerance determining the specific split. This framework has simplified portfolio management whilst providing a coherent theoretical foundation for explaining investment strategies to clients and regulatory authorities.

The practical implementation of CAPM requires careful attention to several technical considerations that can significantly impact its effectiveness. Beta estimation presents particular challenges, as historical relationships may not accurately predict future risk characteristics, especially during periods of structural market change or economic transition. Many practitioners employ adjusted beta calculations that incorporate regression toward the mean tendencies, whilst others utilise fundamental beta estimation techniques based on company-specific operational and financial characteristics.

Risk-free rate selection represents another critical implementation consideration, as the choice of benchmark can materially affect required return calculations. Most applications utilise government treasury securities as risk-free proxies, with the specific maturity selected to match the investment horizon under consideration. However, during periods of financial stress or when analysing international investments, the assumption of truly risk-free government securities may require careful reassessment.

Market portfolio proxy selection similarly affects practical CAPM implementation, as the theoretical market portfolio of all risky assets cannot be directly observed or replicated. Most applications employ broad equity indices such as the S&P 500 as market proxies, though this approach potentially introduces biases when analysing non-equity investments or international securities. Some practitioners employ more comprehensive market proxies that include bonds, real estate, and international assets, though data availability and computational complexity often limit such approaches.

The emergence of factor-based investing strategies represents a significant evolution in CAPM application, acknowledging that additional systematic risk factors beyond market beta may explain security returns. The Fama-French three-factor model and its subsequent extensions incorporate size, value, momentum, and quality factors alongside traditional market risk measures, providing more nuanced approaches to risk-adjusted return analysis. These enhanced models maintain the theoretical framework established by CAPM whilst addressing some of its empirical limitations in explaining cross-sectional return variations.

Regulatory applications of CAPM have proven particularly influential in establishing standards for prudent investment management and fiduciary responsibility. The Prudent Investor Rule, which governs investment decision-making for trust and pension fund management, draws heavily on modern portfolio theory principles established by Markowitz and extended through CAPM. These regulatory frameworks recognise that diversification and systematic risk management, rather than individual security selection, should form the foundation of responsible institutional investment management.

Limitations and Theoretical Criticisms

Despite its theoretical elegance and widespread practical adoption, the Capital Asset Pricing Model faces substantial criticisms that have sparked decades of academic debate and led to the development of numerous alternative asset pricing models. These limitations stem from both the restrictive assumptions underlying CAPM's theoretical construction and empirical evidence suggesting that the model's predictions do not consistently match observed market behaviour across different time periods and market conditions.

The most fundamental criticism of CAPM concerns its reliance on highly restrictive assumptions that appear inconsistent with real-world market behaviour. The model assumes that all investors are rational, risk-averse utility maximisers who possess identical information sets and time horizons—assumptions that behavioural finance research has repeatedly challenged. Real investors demonstrate systematic biases, varying degrees of sophistication, and heterogeneous preferences that can lead to market inefficiencies and pricing anomalies that CAPM cannot explain.

Market efficiency assumptions embedded within CAPM represent another significant limitation, as the model requires that securities markets be perfectly competitive with instantaneous price adjustments to reflect all available information. Empirical evidence suggests that markets exhibit various forms of inefficiency, including momentum effects, mean reversion patterns, and predictable seasonal variations that contradict the efficient market hypothesis underlying CAPM. These inefficiencies create opportunities for active investment strategies that CAPM theory suggests should not exist in equilibrium.

The assumption of constant investment opportunities over time represents a particularly problematic limitation, as CAPM treats risk-free rates, market risk premiums, and beta coefficients as static parameters when they clearly fluctuate substantially over time. The risk-free rate varies continuously with monetary policy decisions and economic conditions, whilst equity risk premiums demonstrate significant cyclical and secular variations that can materially impact expected return calculations. Similarly, individual security and portfolio betas exhibit instability over time, raising questions about the predictive validity of historical beta estimates.

Empirical testing of CAPM has revealed numerous anomalies that challenge the model's explanatory power and practical validity. The size effect, first documented by researchers including Fama and French, demonstrates that small-capitalisation stocks tend to earn higher risk-adjusted returns than CAPM predicts, suggesting that market capitalisation represents an additional systematic risk factor not captured by beta alone. Similarly, the value effect shows that stocks with low price-to-book ratios tend to outperform growth stocks after adjusting for beta risk, indicating that valuation characteristics contain systematic risk information beyond that captured by market sensitivity.

The low-beta anomaly represents perhaps the most direct challenge to CAPM's central prediction, as empirical evidence suggests that low-beta stocks tend to earn higher risk-adjusted returns than high-beta stocks, contradicting the model's fundamental assertion that expected returns should increase linearly with systematic risk. This finding has persisted across different time periods and market conditions, suggesting a fundamental flaw in CAPM's risk-return relationship rather than temporary market inefficiency.

Beta estimation challenges represent significant practical limitations that affect CAPM's implementation effectiveness. Historical beta calculations depend critically on the choice of measurement period, return frequency, and market proxy, with different specifications potentially yielding substantially different beta estimates for the same security. The assumption that historical relationships will persist into the future may be particularly problematic for companies experiencing structural changes, industry disruptions, or significant operational modifications that alter their fundamental risk characteristics.

The single-factor structure of CAPM represents a theoretical limitation that numerous researchers have attempted to address through multi-factor model development. The Arbitrage Pricing Theory, developed by Stephen Ross, provides a more flexible framework that can accommodate multiple systematic risk factors whilst maintaining theoretical consistency. Similarly, the Fama-French factor models and their extensions incorporate additional systematic risk factors including size, value, momentum, and profitability that appear to explain cross-sectional return variations more effectively than beta alone.

Transaction costs and market frictions, explicitly assumed away by CAPM, represent significant practical limitations that affect real-world investment implementation. The model's assumption of unlimited borrowing and lending at the risk-free rate clearly does not hold in practice, as investors face borrowing constraints and credit risk considerations that affect their actual investment opportunities. Similarly, transaction costs, tax considerations, and liquidity constraints can materially affect portfolio construction decisions in ways that CAPM does not address.

International applications of CAPM face additional limitations related to currency risk, market segmentation, and varying regulatory environments that complicate the model's implementation across borders. The International Capital Asset Pricing Model attempts to address some of these concerns by incorporating exchange rate risk as an additional systematic factor, though practical implementation remains challenging due to the complexity of international risk relationships.

Modern Relevance and Theoretical Extensions

The enduring influence of the Capital Asset Pricing Model in contemporary finance extends far beyond its original formulation, serving as the foundational framework from which numerous sophisticated asset pricing models have evolved to address the complexities of modern global financial markets. Whilst academic research has identified significant limitations in CAPM's empirical performance, the model's theoretical insights continue to guide investment practice, regulatory policy, and financial education worldwide, demonstrating the remarkable resilience of its core conceptual contributions.

Modern portfolio management increasingly employs factor-based investing strategies that build upon CAPM's systematic risk framework whilst incorporating additional risk dimensions identified through empirical research. The Fama-French three-factor model represents the most widely adopted extension, adding size and value factors to the original market factor to better explain cross-sectional return variations. This model's success in capturing return patterns that CAPM alone cannot explain has led to its widespread adoption in academic research and practical investment applications, particularly in portfolio performance evaluation and risk-adjusted return analysis.

The evolution toward multi-factor models has accelerated with the development of increasingly sophisticated quantitative investment strategies that seek to harvest systematic risk premiums across multiple dimensions. Modern factor investing encompasses momentum, quality, low-volatility, and profitability factors alongside the traditional size and value characteristics, creating a rich taxonomy of systematic risk sources that extends CAPM's single-factor structure. These developments represent evolutionary refinements rather than revolutionary departures from CAPM's core insights about systematic risk and diversification benefits.

Smart beta and strategic beta investment strategies exemplify how CAPM's theoretical framework continues to influence modern portfolio construction methodology. These approaches maintain CAPM's emphasis on systematic risk management whilst employing alternative weighting schemes designed to capture specific risk premiums or reduce particular risk exposures. The theoretical foundation provided by CAPM enables practitioners to understand these strategies as variations on the fundamental theme of balancing systematic risk exposure with expected return generation.

Risk management applications of CAPM have evolved considerably to address the model's limitations whilst preserving its analytical convenience and theoretical coherence. Modern risk management systems often employ CAPM-derived beta estimates as starting points for more sophisticated risk models that incorporate regime shifts, time-varying parameters, and non-linear risk relationships. These enhanced approaches acknowledge CAPM's limitations whilst leveraging its systematic risk framework to provide practical risk measurement and management tools.

The influence of CAPM on regulatory frameworks and professional standards remains profound, with modern investment regulations continuing to reflect the model's emphasis on diversification and systematic risk management. The Prudent Investor Rule and similar fiduciary standards worldwide incorporate CAPM-inspired concepts about the primacy of asset allocation decisions and the importance of systematic risk management over security selection. These regulatory applications demonstrate how CAPM's theoretical insights have become embedded in the institutional framework governing professional investment management.

Environmental, social, and governance (ESG) investing represents a contemporary application area where CAPM's framework provides valuable analytical structure despite requiring significant conceptual extensions. ESG risk factors can be understood as additional systematic risk dimensions that may command risk premiums in the same manner as traditional financial risk factors. This perspective enables the integration of sustainability considerations into traditional risk-return frameworks whilst maintaining analytical coherence and comparability with conventional investment approaches.

The emergence of alternative risk premiums in hedge fund and institutional investing strategies reflects CAPM's continuing influence on how investment professionals conceptualise systematic risk and return relationships. Strategies focused on harvesting volatility risk premiums, credit risk premiums, and term structure risk premiums all build upon CAPM's fundamental insight that systematic risk exposure should be rewarded with commensurate expected returns. These sophisticated strategies represent natural extensions of CAPM's theoretical framework to new risk dimensions and market segments.

Behavioural finance research has provided important insights into the psychological and institutional factors that can cause departures from CAPM's predictions whilst generally supporting the model's normative implications for rational investment behaviour. Understanding investor biases and market inefficiencies can help explain empirical anomalies in CAPM performance without necessarily invalidating the model's prescriptive value for rational portfolio construction. This research suggests that CAPM may be better understood as a normative model for how investors should behave rather than a positive model of how they actually do behave.

Technology-enabled investment platforms and robo-advisors have made CAPM-inspired portfolio construction accessible to individual investors on an unprecedented scale. Modern portfolio allocation algorithms frequently employ CAPM principles to construct diversified portfolios whilst incorporating behavioural insights and practical constraints that acknowledge real-world implementation challenges. These applications demonstrate how CAPM's theoretical framework can be adapted to serve contemporary investment needs whilst maintaining its core emphasis on systematic risk management and diversification benefits.

International capital market integration has created new opportunities for CAPM application whilst highlighting additional complexities related to currency risk, political risk, and market segmentation effects. Modern international portfolio management increasingly employs CAPM-inspired frameworks that incorporate these additional risk dimensions whilst maintaining the model's systematic approach to risk-return trade-offs. These applications demonstrate the flexibility and adaptability of CAPM's theoretical framework across different market contexts and investment environments.

Conclusion

The Capital Asset Pricing Model stands as one of the most remarkable intellectual achievements in the history of financial economics, representing a rare convergence of theoretical elegance, practical applicability, and profound influence on both academic understanding and professional practice. Developed through the simultaneous efforts of four brilliant economists in the early 1960s, CAPM emerged from Harry Markowitz's foundation in modern portfolio theory to provide the first rigorous framework for understanding how systematic risk should be reflected in expected returns across capital markets. The model's mathematical simplicity—captured in the elegant linear relationship between expected return, beta, and market risk premium—belies its sophisticated theoretical underpinnings and revolutionary implications for investment management.

William Sharpe's emergence as the primary architect of CAPM, culminating in his 1990 Nobel Prize recognition, exemplifies the profound impact that rigorous theoretical work can have on practical financial decision-making. Sharpe's journey from a disappointed graduate student seeking to inject mathematical rigour into financial practice to a Nobel laureate whose insights guide trillions of dollars in investment decisions demonstrates how academic research can fundamentally transform entire industries. His continued contributions to financial theory and practice, including the development of the Sharpe ratio and returns-based style analysis, illustrate the enduring value of the systematic approach to risk and return analysis that CAPM pioneered.

The practical applications of CAPM have proven remarkably durable despite significant theoretical criticisms and empirical challenges. The model's influence on index fund development, regulatory frameworks, and institutional investment management reflects its fundamental insight that diversification represents the primary tool available to investors for managing risk whilst generating appropriate returns. The emergence of factor investing, smart beta strategies, and sophisticated risk management techniques represents evolutionary developments that build upon rather than replace CAPM's core theoretical framework, suggesting that the model's fundamental insights about systematic risk and market efficiency retain significant validity.

The empirical challenges facing CAPM, including the size effect, value premium, and low-beta anomaly, have sparked productive theoretical developments that have enriched rather than undermined the field of financial economics. Multi-factor models, behavioural finance insights, and enhanced risk management techniques all represent attempts to address CAPM's limitations whilst preserving its analytical framework and practical utility. These developments demonstrate the healthy evolution of financial theory in response to empirical evidence whilst maintaining connection to the fundamental principles that CAPM established.

Contemporary applications of CAPM in ESG investing, international portfolio management, and technology-enabled investment platforms demonstrate the model's continuing relevance in addressing modern investment challenges. The framework's flexibility in accommodating new risk factors and market developments suggests that CAPM's influence will persist as financial markets continue to evolve and become increasingly complex. The model's emphasis on systematic risk measurement and diversification benefits provides enduring principles that remain valuable regardless of specific market conditions or technological developments.

The educational impact of CAPM cannot be overstated, as the model continues to provide the foundational framework through which students and professionals develop their understanding of risk and return relationships in financial markets. The model's mathematical tractability and intuitive appeal make it an ideal pedagogical tool whilst its practical applications ensure that theoretical understanding translates into professional competence. This educational legacy ensures that CAPM's insights will continue to influence new generations of investment professionals and academic researchers.

Looking toward the future, CAPM's role in financial theory and practice seems likely to evolve rather than diminish, with the model serving as a benchmark against which more sophisticated approaches can be evaluated and compared. The continuing development of artificial intelligence, machine learning, and big data analytics in investment management provides new tools for implementing CAPM-inspired strategies whilst potentially identifying new systematic risk factors that the model's framework can accommodate. These technological developments may enhance rather than replace the systematic approach to risk and return analysis that CAPM pioneered.

The regulatory and institutional frameworks that incorporate CAPM principles, including fiduciary standards and prudent investor guidelines, provide structural support for the model's continuing influence regardless of academic debates about its empirical performance. These institutional applications reflect the model's value as a systematic approach to investment decision-making that can be consistently applied and objectively evaluated, qualities that remain valuable in professional investment contexts even when more sophisticated models are available.

The Capital Asset Pricing Model ultimately represents more than a mathematical formula or theoretical construct—it embodies a fundamental approach to thinking about investment decisions that emphasises systematic analysis, quantitative methods, and logical consistency. These methodological contributions may prove to be CAPM's most enduring legacy, providing a framework for rational investment decision-making that transcends specific model limitations or empirical challenges. As financial markets continue to evolve and new investment challenges emerge, the analytical approach pioneered by Sharpe, Treynor, Lintner, and Mossin will likely continue to guide both theoretical development and practical application in the ongoing quest to understand and manage the fundamental trade-offs between risk and return in capital markets.

Quote: Merton Miller - Nobel Laureate in Economics

“I favour passive investing for most investors, because markets are amazingly successful devices for incorporating information into stock prices.” - Merton Miller - Nobel Laureate in Economics

Merton Miller, Nobel Laureate in Economics, was a pivotal figure in the development of modern financial theory and a leading advocate for passive investing. The quote, “I favour passive investing for most investors, because markets are amazingly successful devices for incorporating information into stock prices,” encapsulates Miller’s lifelong commitment to highlighting the power and efficiency of financial markets.

About Merton Miller

Miller (1923–2000) was awarded the Nobel Prize in Economic Sciences in 1990, sharing the honour with Harry Markowitz and William Sharpe for ground-breaking work in the field of financial economics. His most influential contribution, alongside Franco Modigliani, was the Modigliani-Miller theorem—a foundational principle which rigorously proved that, under certain conditions, the value of a firm is unaffected by its capital structure. This theorem underpinned the belief that markets price information efficiently and forms an intellectual basis for the case for passive investing.

Beyond his Nobel-winning research, Miller was renowned for his candid commentary on investing. He consistently argued that, while individual investors might believe they possess superior insights, markets—comprised of thousands of informed participants—collectively synthesise information so effectively that it becomes extremely difficult for any single investor to outperform the index after costs. As he famously quipped, “Everybody has some information. The function of the markets is to aggregate that information, evaluate it and get it incorporated into prices”.

Context of the Quote

The quote is a summation of decades of academic research and market observation. Miller, reflecting on the odds of outperforming the market, reasoned that for “most investors”, passive investing is the only rational route. He noted the steep costs of active management—not just fees, but the resources required to “dig up information no one else has yet”. For Miller, market prices reflected the best available information, making attempts to “pick winners” a game of chance rather than skill for the majority.

This view gained substantial traction, especially as the academic tradition moved toward the concept of market efficiency. Miller warned pension fund managers that failing to allocate the majority of their portfolios to passive strategies—typically 70–80%, by his estimation—was not just suboptimal, but potentially a breach of fiduciary duty.

Leading Theorists in Passive Investing and Market Efficiency

The academic roots of passive investing run deep, with a lineage of Nobel Laureates and theorists who shaped the discipline:

• Eugene Fama: Often called the ‘father of the Efficient Market Hypothesis (EMH)’, Fama empirically demonstrated that markets are largely efficient, quickly reflecting all publicly available information in asset prices. This theory provides the intellectual justification for index investing and the idea that beating the market is exceptionally difficult for most investors.

• Harry Markowitz: Awarded the Nobel in 1990 alongside Miller, Markowitz’s work on Modern Portfolio Theory showed how diversification can minimise unsystematic risk. His ideas underpinned the structure of index funds, designed to capture broad market returns rather than pursue potentially elusive ‘alpha’.

• William Sharpe: Another 1990 Nobel Laureate, Sharpe introduced the Capital Asset Pricing Model (CAPM), which articulated the relationship between risk and expected return. Sharpe was an early proponent of index funds and highlighted the drag of management fees on investor outcomes, recommending that expense ratio should be a key screening criterion for investors.

• John Bogle: Although not an academic, Bogle was the founder of Vanguard and the pioneer of the first index mutual fund. His philosophy—“Don’t look for the needle in the haystack; just buy the haystack”—embodied the joint lessons of market efficiency and diversification.

• Michael Mauboussin and Andrei Shleifer: Recent voices have further nuanced the debate, discussing the effects of passive flows on share prices and revisiting demand curve theory in stock markets. While the consensus remains in favour of passive investing for most, ongoing dialogue underscores both the robustness and the boundaries of market efficiency.

Broader Context

The shift towards passive investing is not merely theoretical but has reshaped global markets. Decades of empirical research confirm Miller’s central insight: most investors “might just as well buy a share of the whole market, which pools all the information, than delude themselves into thinking they know something the market doesn’t”. Despite periodic debate—such as whether passive investing could itself distort markets—the evidence and leading academic voices overwhelmingly endorse its primacy for the majority of investors.

Key Themes

• Market Efficiency: Prices reflect available information; isolated investor insight is rarely enough to reliably outperform.

• Diversification: Passive instruments such as index funds enable broad market exposure and risk minimisation—a tenet shared by Markowitz and Miller.

• Cost Effectiveness: High fees persistently erode returns; passive strategies offer a more efficient alternative for most.

• Fiduciary Duty: Miller asserted that those responsible for large pools of savings, such as pension funds, are ethically and practically compelled to choose passive allocations.

Summary Table: Leading Theorists in Passive Investing

Merton Miller’s quote stands not as a passing remark, but as the distilled wisdom of a career devoted to understanding and proving the power of markets. It is a touchstone statement for a generation of investors and fiduciaries committed to evidence over speculation, and efficiency over expense.

Term: Weighted Average Cost of Capital (WACC)

The Weighted Average Cost of Capital (WACC) stands as one of the most fundamental and influential concepts in modern corporate finance, representing the blended cost of all capital sources a company employs to fund its operations and growth initiatives. This comprehensive metric, which integrates the costs of debt, equity, and preferred stock according to their proportional weights in a firm's capital structure, serves as a critical benchmark for investment decisions, corporate valuation, and strategic financial planning. The theoretical underpinnings of WACC trace back to the groundbreaking work of economists Franco Modigliani and Merton Miller, whose capital structure propositions in the late 1950s revolutionised corporate finance theory and established the intellectual framework upon which WACC calculations are built. Their seminal research demonstrated that under certain idealised conditions, a firm's value remains independent of its capital structure, whilst also revealing how real-world factors such as taxation, bankruptcy costs, and information asymmetries create opportunities for optimal capital structure decisions that directly impact WACC calculations. Today, WACC functions not merely as an academic construct but as a practical tool employed by corporate executives, investment analysts, and strategic advisors to evaluate project feasibility, determine appropriate discount rates for discounted cash flow analyses, and assess the relative attractiveness of different financing strategies in an increasingly complex global financial landscape.

Historical Context and Theoretical Foundations

The conceptual foundation underlying WACC calculations emerged from a revolutionary period in academic finance during the mid-20th century, when traditional approaches to corporate finance were being fundamentally challenged by rigorous economic theory. Prior to this transformation, corporate finance decisions were often guided by rules of thumb and conventional wisdom rather than systematic theoretical frameworks. The landscape began to shift dramatically with the introduction of the Modigliani-Miller theorem, which provided the first comprehensive theoretical analysis of how capital structure decisions affect firm valuation.

Franco Modigliani and Merton Miller's initial proposition, published in 1958, fundamentally challenged prevailing notions about optimal capital structure by demonstrating that under perfect market conditions—characterised by the absence of taxes, bankruptcy costs, agency costs, and asymmetric information—a firm's value remains entirely independent of its financing decisions. This seemingly counterintuitive finding suggested that whether a company funded its operations through debt, equity, or any combination thereof, its overall enterprise value would remain constant. The theorem's elegant mathematical proof relied on arbitrage arguments, showing that investors could replicate any corporate financing decision in their personal portfolios, thereby eliminating any potential value creation from capital structure choices.

However, the true power of the Modigliani-Miller framework emerged not from its initial proposition but from its subsequent refinements that acknowledged real-world market imperfections. The second iteration of their work, incorporating corporate taxation, revealed that debt financing could indeed create value through the tax deductibility of interest payments. This insight established the theoretical basis for what would later become the interest tax shield component of WACC calculations, demonstrating that the after-tax cost of debt should be lower than its nominal cost due to the tax benefits associated with interest payments.

The implications of this refined Modigliani-Miller theorem extended far beyond academic theory, establishing the intellectual groundwork for modern approaches to capital structure optimisation. By recognising that tax considerations create a genuine preference for debt financing—at least up to a certain point—the theorem provided the theoretical justification for the weighted average approach that characterises WACC calculations. The framework demonstrated that companies could potentially reduce their overall cost of capital by strategically balancing the tax advantages of debt against the increased financial risk and potential distress costs associated with higher leverage.

This theoretical evolution coincided with broader developments in financial economics, including the emergence of portfolio theory and the capital asset pricing model, which provided sophisticated methods for estimating the cost of equity capital. These complementary theoretical advances created the comprehensive framework necessary for practical WACC calculations, combining insights about optimal capital structure with quantitative methods for determining the required returns on different types of capital. The convergence of these theoretical streams established WACC as both a conceptually sound and practically implementable tool for corporate financial decision-making.

Components and Mathematical Framework of WACC

The calculation of WACC requires a sophisticated understanding of its constituent components, each of which presents unique challenges in terms of measurement and estimation. The fundamental WACC formula, expressed as WACC = (E/V × Re) + (D/V × Rd × (1 - Tc)), encapsulates the weighted contribution of each capital source to the firm's overall cost of capital. This deceptively simple equation masks considerable complexity in the determination of each component, requiring careful attention to market values, risk assessments, and tax considerations.

The weighted average cost of capital (WACC) is the average rate a company must pay to all its capital providers—including both equity investors and lenders—weighted by the proportion each source represents in the firm's capital structure, and is commonly used as the discount rate in valuing investments and determining a business’s required rate of return.

The cost of equity component represents perhaps the most challenging element of WACC calculations, as equity capital lacks the explicit contractual terms that characterise debt instruments. Unlike debt, where interest rates provide a clear indication of the cost of capital, equity investors' required returns must be inferred from market data and theoretical models. The Capital Asset Pricing Model (CAPM) serves as the predominant framework for estimating the cost of equity, expressing this cost as the sum of a risk-free rate and a risk premium determined by the stock's beta coefficient and the market risk premium.

The CAPM approach begins with the identification of an appropriate risk-free rate, typically derived from government securities with maturities matching the investment horizon under consideration. The selection of the risk-free rate requires careful attention to market conditions and the specific context of the analysis, as rates can vary significantly across different time periods and economic environments. The model then incorporates the stock's beta coefficient, which measures the systematic risk of the investment relative to the broader market. Beta estimation involves statistical analysis of historical stock price movements relative to a market index, though this backward-looking approach may not fully capture future risk characteristics.

The equity risk premium, representing the additional return that investors demand for bearing systematic market risk, requires estimation based on historical market data or forward-looking indicators. This component of the cost of equity calculation has proven particularly contentious among practitioners, as historical risk premiums may not accurately reflect future market conditions. Some analysts prefer to use implied risk premiums derived from current market valuations, whilst others rely on long-term historical averages or survey-based estimates of investor expectations.

Alternative approaches to estimating the cost of equity include the dividend capitalisation model, which derives required returns from dividend payments and expected growth rates. This method proves particularly useful for companies with established dividend policies and stable growth patterns. The dividend capitalisation model expresses the cost of equity as the sum of the dividend yield and the expected dividend growth rate, providing a more direct link between current market conditions and required returns. However, this approach becomes less reliable for companies that do not pay dividends or have highly variable dividend policies.

The cost of debt component typically proves more straightforward to calculate than the cost of equity, as it reflects the explicit interest rates that companies pay on their borrowing. For companies with publicly traded debt, the cost of debt can be estimated using the yield to maturity on outstanding bonds, adjusted for any differences between the current credit rating and the rating at the time of issuance. Companies without publicly traded debt require alternative approaches, such as examining the borrowing costs of similarly rated companies or estimating credit spreads based on financial metrics and credit ratings.

The tax shield benefit associated with debt financing represents a crucial component of WACC calculations, reflecting the value created by the tax deductibility of interest payments. The after-tax cost of debt, calculated as Rd × (1 - Tc), captures this benefit by reducing the effective cost of debt financing. However, the realisation of tax benefits depends on the company's ability to generate sufficient taxable income to utilise the interest deductions, a consideration that becomes particularly important for companies with volatile earnings or those operating in low-tax jurisdictions.

The determination of appropriate weights for debt and equity requires market-based valuations rather than book values, as market values better reflect the current cost and availability of different types of capital. The market value of equity typically equals the current stock price multiplied by the number of outstanding shares, though complications can arise from employee stock options, convertible securities, and other complex capital instruments. The market value of debt proves more challenging to determine, particularly for companies with complex debt structures or privately negotiated borrowing arrangements. Many practitioners approximate debt market values using book values, adjusted for any significant changes in interest rates since the debt was issued.

Applications in Corporate Finance and Investment Analysis

WACC serves as a cornerstone metric in numerous corporate finance applications, functioning primarily as a discount rate for discounted cash flow analyses and as a benchmark for evaluating investment opportunities. In the context of discounted cash flow valuation, WACC represents the appropriate discount rate for free cash flows to the firm, reflecting the blended cost of capital that all stakeholders require for their investment in the company. This application proves particularly valuable in merger and acquisition analysis, where acquirers must determine the present value of target companies' future cash flows to establish appropriate offer prices.

The use of WACC as a hurdle rate for capital budgeting decisions represents another fundamental application in corporate finance practice. Companies typically require that new investment projects generate returns exceeding their WACC to ensure that these investments create value for shareholders. Projects with expected returns below the WACC may actually destroy shareholder value by diverting capital from higher-returning alternatives available in financial markets. This hurdle rate approach provides a systematic framework for comparing investment opportunities across different divisions, time periods, and risk profiles within a single organisation.

However, the application of a single WACC across all projects within a company raises important questions about risk adjustment and project-specific factors. Different business segments may face varying degrees of systematic risk, competitive pressures, and market conditions that warrant different discount rates. Some companies address this challenge by calculating divisional WACCs that reflect the specific risk profiles and capital structures typical of different business lines. This approach requires careful analysis of comparable companies operating in each business segment, along with adjustments for differences in capital structure and operating leverage.

The relationship between WACC and company valuation extends beyond simple discounting applications to encompass broader strategic considerations about optimal capital structure. Companies seeking to maximise their market valuation must consider how changes in their debt-to-equity ratios affect their WACC, balancing the tax advantages of additional debt against the increased financial risk and potential distress costs. This optimisation process, grounded in the trade-off theory of capital structure, recognises that the benefits of leverage eventually diminish as companies approach levels where financial distress becomes a significant concern.

Economic Value Added (EVA) calculations represent another sophisticated application of WACC in corporate finance, measuring the value created by management decisions relative to the cost of capital. EVA analysis subtracts a capital charge, calculated as WACC multiplied by invested capital, from operating profits to determine whether management has created or destroyed shareholder value during a specific period. This performance measurement framework has gained widespread adoption among companies seeking to align management incentives with shareholder value creation objectives.

The application of WACC in strategic planning and corporate development requires careful consideration of how different strategic initiatives might affect the company's cost of capital over time. Major acquisitions, divestitures, or changes in business strategy can significantly alter a company's risk profile and optimal capital structure, necessitating periodic recalculation of WACC. Strategic planners must anticipate these changes when evaluating long-term investment programmes or considering fundamental shifts in business focus.

International applications of WACC introduce additional complexity related to currency risk, political risk, and differences in tax systems and capital market development. Companies operating in multiple countries must decide whether to use a single global WACC or to calculate country-specific discount rates that reflect local market conditions and risks. The choice between these approaches depends on factors such as the degree of integration between the company's operations in different countries, the availability of local financing sources, and the extent to which cash flows can be repatriated across borders.

The Trade-Off Theory and Capital Structure Optimisation

The trade-off theory of capital structure provides the theoretical foundation for understanding how WACC varies with changes in financial leverage and how companies can potentially optimise their capital structure to minimise their cost of capital. This theory recognises that whilst debt financing offers tax advantages through deductible interest payments, increasing levels of leverage also introduce costs related to financial distress, agency conflicts, and reduced financial flexibility. The optimal capital structure represents the point where the marginal benefits of additional debt exactly offset the marginal costs, resulting in the lowest possible WACC and highest firm valuation.

The tax shield component of the trade-off theory directly influences WACC calculations through the after-tax cost of debt term in the standard formula. As companies increase their use of debt financing, they initially benefit from the tax deductibility of interest payments, which reduces their overall cost of capital. However, this benefit is not unlimited, as it depends on the company's ability to generate sufficient taxable income to utilise the interest deductions fully. Companies with volatile earnings or those operating in industries with significant cyclical fluctuations may find that their ability to capture tax benefits varies considerably over time.

Financial distress costs represent the primary constraint on leverage in the trade-off theory, encompassing both direct costs such as bankruptcy proceedings and legal fees, and indirect costs such as the loss of customers, suppliers, and key employees when financial difficulties become apparent. These costs are difficult to quantify precisely but can be substantial for companies in industries where reputation and ongoing relationships are critical to business success. The anticipation of financial distress costs by investors and creditors typically manifests as higher required returns on both debt and equity as leverage increases beyond moderate levels.

Agency costs constitute another important element of the trade-off theory, arising from conflicts of interest between different classes of stakeholders. Higher levels of debt can create agency costs of debt, where shareholders have incentives to pursue risky projects that transfer value from bondholders to equity holders. Conversely, debt can also reduce agency costs of equity by constraining management's ability to pursue value-destroying projects or excessive perquisites. The net effect of these competing agency considerations depends on the specific governance structure and incentive systems within individual companies.

The practical application of trade-off theory in WACC optimisation requires careful analysis of industry characteristics, company-specific factors, and market conditions. Companies in stable, mature industries with predictable cash flows typically can support higher levels of leverage than those in cyclical or rapidly growing industries. Similarly, companies with substantial tangible assets that can serve as collateral may be able to borrow at more favourable rates and sustain higher debt levels than asset-light companies in service industries.

Market timing considerations can also influence optimal capital structure decisions and their impact on WACC. Companies may find it advantageous to issue debt when interest rates are particularly low or to issue equity when their stock price is at historical highs. These tactical considerations can temporarily move companies away from their long-term optimal capital structure, though the theory suggests that companies should eventually revert to their target leverage ratios as market conditions normalise.

The dynamic nature of optimal capital structure means that companies must periodically reassess their target debt-to-equity ratios and corresponding WACC calculations. Changes in the business environment, tax regulations, or company-specific factors such as growth prospects or asset composition can shift the optimal balance between debt and equity financing. Companies that fail to adjust their capital structure in response to these changes may find themselves operating with suboptimal cost of capital and reduced firm valuation.

Limitations and Practical Challenges in WACC Implementation

Despite its widespread acceptance and utility, WACC calculations face numerous limitations and practical challenges that can significantly affect their accuracy and applicability. The most fundamental limitation stems from the inherent uncertainty in estimating several key components of the calculation, particularly the cost of equity and the appropriate weights for different capital sources. These estimation challenges can lead to significant variations in calculated WACC values, depending on the specific assumptions and methodologies employed.

The estimation of beta coefficients for the cost of equity calculation presents particular difficulties, as these measures of systematic risk are based on historical data that may not accurately reflect future risk characteristics. Beta calculations require sufficiently long time series of stock price data to generate statistically reliable estimates, yet longer time periods may incorporate outdated information that no longer reflects the company's current risk profile. Additionally, companies that have undergone significant structural changes, such as major acquisitions or strategic repositioning, may find that historical beta estimates provide poor guidance for future risk assessment.

The choice of market risk premium represents another source of uncertainty in cost of equity calculations, with different estimation methods often yielding substantially different results. Historical risk premiums based on long-term market returns may not reflect current market conditions or investor expectations, whilst forward-looking measures derived from analyst forecasts or option pricing models may be influenced by temporary market conditions or systematic biases in expectations. This uncertainty in risk premium estimation can have substantial impacts on calculated WACC values, as the risk premium is multiplied by the company's beta coefficient.

The treatment of preferred stock and other hybrid securities in WACC calculations introduces additional complexity, as these instruments often combine characteristics of both debt and equity. Preferred stock typically pays fixed dividends like debt but ranks junior to debt in bankruptcy proceedings like equity. The appropriate treatment of such instruments requires careful analysis of their specific terms and conditions, as well as consideration of how they are perceived by investors and rating agencies.

Market value estimation for debt components can prove challenging, particularly for companies with complex debt structures involving multiple tranches, covenants, and embedded options. Private debt agreements may lack observable market prices, requiring approximation based on comparable publicly traded instruments or credit rating-based estimates. Additionally, off-balance-sheet obligations such as operating leases, pension obligations, and other contingent liabilities may require inclusion in debt calculations under certain circumstances, though the appropriate treatment of these items remains a matter of professional judgement.

The assumption of constant capital structure weights inherent in most WACC calculations may not reflect the dynamic nature of many companies' financing strategies. Companies frequently adjust their capital structure in response to market conditions, growth opportunities, or changes in their business risk profile. Using current market values to determine weights may therefore provide a snapshot that quickly becomes outdated, whilst using target weights requires accurate assessment of management's long-term capital structure objectives.

Cyclical variations in market conditions can significantly affect WACC calculations, particularly during periods of financial market stress or unusual economic conditions. Credit spreads, equity risk premiums, and risk-free rates can all fluctuate substantially over short periods, leading to significant variations in calculated WACC values. Companies must decide whether to use current market conditions or to attempt to normalise for temporary market distortions when calculating their cost of capital.

The application of a single WACC to evaluate projects with different risk profiles represents a fundamental limitation of the traditional approach. Companies operating in multiple business segments or considering investments in new markets may find that a single hurdle rate fails to capture the varying risk characteristics of different opportunities. This limitation has led to the development of divisional WACC calculations and risk-adjusted discount rate approaches, though these refinements introduce their own complexities and estimation challenges.

Currency and international considerations add another layer of complexity for multinational companies. Exchange rate volatility, political risks, and differences in tax systems across countries can all affect the appropriate cost of capital for international investments. Companies must decide whether to use domestic WACC calculations adjusted for international risks or to develop country-specific discount rates based on local market conditions.

Real-World Implementation and Case Studies

The practical implementation of WACC calculations in real-world corporate environments reveals the complexities and nuances that distinguish theoretical frameworks from operational reality. Major corporations typically develop sophisticated processes for WACC calculation that involve multiple departments, external consultants, and regular review cycles to ensure accuracy and relevance. These processes must balance theoretical rigour with practical constraints such as data availability, resource limitations, and the need for timely decision-making.

Large technology companies provide particularly interesting case studies in WACC implementation due to their unique capital structure characteristics and growth profiles. Apple Inc., for instance, maintains substantial cash reserves alongside its debt financing, creating complexities in determining the appropriate market values for WACC calculations. The company's WACC calculation must account for its substantial foreign cash holdings, complex international tax planning strategies, and the rapid evolution of its business model from primarily hardware-focused to increasingly service-oriented. Analysts estimating Apple's cost of equity must grapple with the company's transition from a high-growth technology company to a more mature dividend-paying corporation, which affects both beta estimation and growth rate assumptions.

Manufacturing companies face different challenges in WACC implementation, particularly in industries characterised by substantial capital intensity and cyclical demand patterns. The automotive industry exemplifies these challenges, where companies must balance the benefits of debt financing for large capital investments against the risks associated with cyclical downturns that can severely impact cash flows and debt service capabilities. Ford Motor Company's WACC calculations, for example, must account for the company's pension obligations, the cyclical nature of automotive demand, and the substantial capital requirements for transitioning to electric vehicle production.

The financial services industry presents unique challenges for WACC calculation due to the heavily regulated nature of the business and the different role that leverage plays compared to other industries. For banks and insurance companies, debt represents both a funding source and a primary business input, as these institutions profit from the spread between their borrowing costs and lending rates. Regulatory capital requirements also introduce constraints on capital structure that may override pure economic optimisation considerations, requiring adjustments to traditional WACC frameworks.

Utility companies offer insights into WACC implementation in heavily regulated industries where cost of capital calculations directly influence regulatory rate-setting processes. Electric utilities must typically justify their WACC calculations to regulatory authorities as part of rate case proceedings, requiring detailed documentation of all assumptions and methodologies. The regulated nature of these businesses typically results in more stable and predictable cash flows, which can support higher leverage ratios and potentially lower overall cost of capital. However, regulatory lag and the need for substantial infrastructure investments create unique considerations for WACC calculation and application.

Private equity firms and leveraged buyout transactions demonstrate WACC concepts in highly leveraged capital structures designed to maximise returns while managing financial risk. These transactions typically involve careful optimisation of capital structure to minimise WACC whilst maintaining adequate financial flexibility to execute operational improvements and strategic initiatives. The temporary nature of many private equity investments also requires consideration of how capital structure and WACC may evolve as companies prepare for eventual exit through public offerings or strategic sales.

Start-up and high-growth companies face particular challenges in WACC calculation due to limited operating history, uncertain cash flows, and rapidly evolving business models. Traditional beta estimation becomes problematic for companies with short public trading histories, requiring the use of comparable company analysis or other proxy methods. The high growth rates typical of these companies also complicate the estimation of appropriate discount rates, as investors may require substantial risk premiums to compensate for the uncertainty associated with unproven business models and competitive positions.

International case studies reveal additional complexities in WACC implementation across different regulatory and market environments. European companies operating under different accounting standards and tax regimes must adapt WACC methodologies to reflect local market conditions and regulatory requirements. Emerging market companies face additional challenges related to political risk, currency volatility, and less developed capital markets that may limit the availability of reliable market data for WACC calculations.

Franco Modigliani and Merton Miller: The Theoretical Pioneers

The development of WACC as a cornerstone concept in corporate finance is inseparable from the groundbreaking contributions of Franco Modigliani and Merton Miller, two economists whose collaborative work in the late 1950s fundamentally transformed the academic understanding of capital structure and corporate valuation. Their partnership, which began during their tenure at Carnegie Mellon University's Graduate School of Industrial Administration, produced theoretical insights that continue to influence corporate finance practice more than six decades after their initial publication.

Franco Modigliani's journey to becoming one of the most influential economists of the 20th century began in turbulent circumstances that shaped both his intellectual development and his approach to economic theory. Born in Rome in 1918, Modigliani experienced firsthand the rise of fascism in his native Italy, which ultimately forced him to flee to the United States in 1939 due to his Jewish heritage and anti-fascist political views. This early experience with political upheaval instilled in Modigliani a deep appreciation for the stability and intellectual freedom that characterised American academic institutions, influencing his lifelong commitment to rigorous economic analysis and policy-relevant research.

Modigliani's academic career in the United States began at the New School of Social Research, where he completed his doctoral studies in 1944 under the supervision of economists who were themselves refugees from European fascism. This intellectual environment, characterised by a blend of European theoretical sophistication and American empirical pragmatism, profoundly influenced Modigliani's approach to economic research. His early work focused on macroeconomic theory, particularly the development of what would become known as the life-cycle hypothesis of consumption, which earned him recognition as a leading authority on household saving behaviour and macroeconomic modelling.

The life-cycle hypothesis represented Modigliani's first major contribution to economic theory, proposing that individuals plan their consumption and saving decisions over their entire lifetime rather than responding solely to current income levels. This insight provided a microeconomic foundation for understanding aggregate saving patterns and their implications for economic growth and stability. The theory suggested that young people typically borrow against future income, middle-aged individuals accumulate wealth for retirement, and elderly people spend down their accumulated assets, creating predictable patterns of saving behaviour across different age cohorts.

Modigliani's transition from macroeconomic theory to corporate finance occurred during his tenure at Carnegie Mellon University, where he encountered Merton Miller and began the collaboration that would revolutionise corporate finance theory. The partnership proved synergistic, combining Modigliani's theoretical sophistication with Miller's practical understanding of financial markets and institutional considerations. Their joint work addressed fundamental questions about how financing decisions affect firm value, challenging conventional wisdom that had previously gone unexamined by rigorous economic analysis.

Merton Miller's background provided the perfect complement to Modigliani's theoretical orientation, bringing a practical understanding of financial markets and institutions that grounded their theoretical work in real-world considerations. Born in Boston in 1923, Miller's early career included practical experience in government service, working as an economist at the US Treasury Department and the Federal Reserve System before pursuing academic research. This exposure to policy-making and financial market operations provided Miller with insights into the practical constraints and institutional factors that influence corporate financing decisions.

Miller's doctoral work at Johns Hopkins University focused on empirical economic analysis, developing skills in statistical methods and data analysis that proved crucial to the collaborative work with Modigliani. The combination of practical experience and rigorous analytical training positioned Miller to bridge the gap between theoretical economic principles and their practical implementation in corporate finance. His understanding of institutional factors such as tax regulations, bankruptcy procedures, and market microstructure considerations ensured that the theoretical framework he developed with Modigliani remained relevant to practitioners.

The initial Modigliani-Miller proposition, published in 1958 in the American Economic Review, fundamentally challenged prevailing views about optimal capital structure by demonstrating that under idealised conditions, firm value remains independent of financing decisions. The theorem's proof relied on arbitrage arguments, showing that investors could replicate any corporate capital structure decision in their personal portfolios, thereby eliminating any potential value creation from financing choices. This seemingly counterintuitive result forced both academics and practitioners to reconsider their basic assumptions about corporate finance and to identify the specific market imperfections that create opportunities for value-enhancing financing decisions.

The second Modigliani-Miller proposition, which incorporated corporate taxation, provided the theoretical foundation for modern WACC calculations by demonstrating that the tax deductibility of interest payments creates a genuine preference for debt financing. This refinement showed that the value of a levered firm equals the value of an otherwise identical unlevered firm plus the present value of the tax shield created by debt financing. The implication for cost of capital calculations was profound, establishing that the after-tax cost of debt should be used in WACC computations and providing theoretical justification for the tax adjustment factor that remains a cornerstone of modern WACC methodology.

The intellectual courage required to challenge established orthodoxies in corporate finance cannot be overstated, as both Modigliani and Miller faced significant scepticism from academics and practitioners who found their conclusions difficult to accept. The apparent disconnect between the theorem's predictions and observed corporate behaviour led to extensive debate and research aimed at identifying the market imperfections that explain real-world capital structure patterns. This scholarly dialogue ultimately enriched the field by spurring development of more sophisticated theories that incorporate factors such as bankruptcy costs, agency problems, and information asymmetries.

The recognition of Modigliani and Miller's contributions came through the highest honours available to economists, with both scholars receiving Nobel Prize recognition for their work. Modigliani received the 1985 Nobel Prize in Economic Sciences not only for the capital structure theorem but also for his contributions to consumption theory and macroeconomic modelling. Miller shared the 1990 Nobel Prize in Economic Sciences with Harry Markowitz and William Sharpe, with the Nobel Committee specifically recognising his fundamental contributions to corporate finance theory. The delay between their collaborative work and Nobel recognition reflects the time required for the academic community to fully appreciate the profound implications of their theoretical insights.

The personal characteristics and working relationship between Modigliani and Miller contributed significantly to their collaborative success. Modigliani's theoretical sophistication and Miller's practical understanding created a productive tension that pushed their analysis in directions neither might have pursued independently. Their different backgrounds—Modigliani's European intellectual training and Miller's American empirical orientation—ensured that their theoretical work addressed both conceptual elegance and practical relevance. The mutual respect and intellectual chemistry between the two scholars enabled them to persist through the intensive analytical work required to develop their groundbreaking propositions.

The legacy of Modigliani and Miller extends far beyond their specific theoretical contributions to encompass their influence on the entire field of corporate finance. Their work established corporate finance as a rigorous academic discipline grounded in economic theory rather than institutional description or rules of thumb. The analytical framework they developed continues to provide the conceptual foundation for advanced topics in corporate finance, including WACC calculations, capital structure optimisation, and valuation methodology. Contemporary developments in corporate finance, from behavioural finance to market microstructure analysis, build upon the theoretical foundation that Modigliani and Miller established.

Contemporary Relevance and Future Implications

The relevance of WACC in contemporary corporate finance has evolved significantly in response to changing market conditions, regulatory environments, and business models that characterise the modern global economy. The low interest rate environment that persisted in many developed economies following the 2008 financial crisis created unique challenges and opportunities for WACC calculation and application. Ultra-low risk-free rates compressed the cost of debt for many companies whilst simultaneously reducing the denominator in equity risk premium calculations, creating complex interactions that affected overall cost of capital estimates.

The emergence of environmental, social, and governance (ESG) considerations in investment decision-making has begun to influence WACC calculations as investors increasingly incorporate sustainability factors into their required return calculations. Companies with strong ESG profiles may benefit from lower cost of capital as institutional investors demonstrate preferences for sustainable investments, whilst companies with poor ESG performance may face higher funding costs as certain investor classes exclude them from consideration. This trend suggests that future WACC calculations may need to explicitly incorporate ESG risk premiums or discounts to accurately reflect market pricing of different types of capital.

Technological disruption across industries has created new challenges for WACC estimation, particularly for companies undergoing rapid digital transformation or facing disruption from new business models. Traditional comparable company analysis becomes problematic when entire industries are experiencing fundamental changes in their competitive dynamics, customer relationships, and value creation mechanisms. Companies in sectors such as retail, media, and transportation must grapple with how digital transformation affects their systematic risk profiles and appropriate cost of capital.

The increasing importance of intangible assets in modern business models poses particular challenges for WACC application, as traditional valuation frameworks were developed primarily for asset-intensive industries. Technology companies, pharmaceutical firms, and other knowledge-based enterprises may find that their risk profiles differ significantly from historical patterns, requiring adjustments to beta estimation methodologies and potentially different approaches to capital structure optimisation. The difficulty of using intangible assets as collateral for debt financing may also affect optimal capital structure decisions and their impact on WACC.

Globalisation and the increasing integration of international financial markets have created opportunities for multinational companies to optimise their cost of capital through strategic financing decisions across different markets. Companies can potentially reduce their WACC by accessing lower-cost capital in international markets, though they must balance these benefits against additional risks such as currency exposure, political risk, and regulatory complexity. The development of international bond markets and the increasing sophistication of currency hedging instruments have expanded the opportunities for global capital structure optimisation.

The growth of alternative financing sources, including private debt markets, sovereign wealth funds, and alternative asset managers, has expanded the range of capital sources available to companies whilst potentially affecting WACC calculations. These alternative sources often have different risk preferences, return requirements, and investment horizons compared to traditional bank lenders and public equity investors. Companies accessing these markets may need to adjust their WACC calculations to reflect the specific characteristics and requirements of these alternative capital providers.

Central bank policies and their impact on financial market conditions continue to influence WACC calculations across all industries and geographies. Quantitative easing programmes, forward guidance on interest rates, and other unconventional monetary policies can create distortions in traditional relationships between risk-free rates, credit spreads, and equity risk premiums. Companies and analysts must consider whether current market conditions reflect sustainable long-term relationships or temporary distortions that require adjustment in WACC calculations.

The increasing frequency and severity of economic disruptions, from financial crises to global pandemics, have highlighted the importance of scenario analysis and stress testing in WACC applications. Companies are increasingly required to consider how their cost of capital might change under different economic scenarios and to incorporate these considerations into their capital allocation and risk management decisions. This trend toward more sophisticated risk analysis suggests that future WACC applications may involve multiple scenarios and dynamic adjustment mechanisms rather than single-point estimates.

Regulatory developments continue to influence WACC calculations across various industries, from banking capital requirements to utility rate-setting procedures. The implementation of international accounting standards, changes in tax regulations, and evolving approaches to systemic risk regulation all affect the inputs and applications of WACC calculations. Companies operating in regulated industries must maintain particular vigilance regarding how regulatory changes might affect their cost of capital and optimal capital structure decisions.

The democratisation of financial information and analytical tools through technology platforms has made sophisticated WACC calculations more accessible to smaller companies and individual investors. Cloud-based analytical platforms, automated data feeds, and artificial intelligence-powered analysis tools are reducing the barriers to implementing sophisticated cost of capital calculations. This trend may lead to more widespread and standardised application of WACC concepts across a broader range of companies and investment decisions.

Conclusion

The Weighted Average Cost of Capital stands as one of the most enduring and influential concepts in modern corporate finance, bridging theoretical sophistication with practical applicability in ways that few financial metrics achieve. From its theoretical origins in the groundbreaking work of Franco Modigliani and Merton Miller to its contemporary applications across diverse industries and global markets, WACC has demonstrated remarkable adaptability whilst maintaining its core conceptual integrity. The metric's ability to synthesise complex information about market conditions, company-specific risks, and financing decisions into a single, actionable measure explains its persistence as a cornerstone tool for corporate executives, investment analysts, and strategic advisors.

The comprehensive examination of WACC presented in this analysis reveals both the metric's substantial strengths and its inherent limitations. The theoretical foundation provided by the Modigliani-Miller theorem offers intellectual rigour and conceptual clarity that has withstood decades of scrutiny and refinement. Their insight that capital structure matters primarily through market imperfections such as taxation, bankruptcy costs, and agency problems continues to provide the analytical framework for understanding why WACC calculations remain relevant and valuable for corporate decision-making. The tax shield benefits incorporated in after-tax cost of debt calculations, the systematic risk adjustments embedded in cost of equity estimates, and the market value weighting approach all reflect theoretical insights that have proven their practical worth through extensive real-world application.

Yet the practical challenges associated with WACC implementation cannot be understated. The difficulties inherent in estimating cost of equity through beta calculations and risk premium determinations, the complexities involved in determining appropriate market value weights for different capital sources, and the assumptions required to apply single discount rates across diverse project portfolios all highlight the gap between theoretical elegance and operational reality. These challenges require sophisticated judgement, extensive market knowledge, and careful attention to the specific circumstances of individual companies and investment decisions.

The evolution of WACC applications in response to changing market conditions, regulatory environments, and business models demonstrates the metric's fundamental robustness whilst highlighting areas requiring continued development. The incorporation of ESG considerations into cost of capital calculations, the challenges posed by digital transformation and intangible asset-intensive business models, and the opportunities created by globalised capital markets all suggest directions for future refinement and enhancement of WACC methodologies. These developments require practitioners to balance theoretical consistency with practical adaptation to emerging market realities.

The legacy of Franco Modigliani and Merton Miller extends far beyond their specific contributions to capital structure theory, encompassing their transformation of corporate finance from a primarily descriptive field to a rigorous academic discipline grounded in economic theory. Their intellectual courage in challenging established orthodoxies, their commitment to theoretical rigour, and their recognition of practical constraints established a model for academic research that continues to influence the field. The Nobel Prize recognition accorded to both scholars reflects not only their individual contributions but also the profound impact of their collaborative work on the development of modern finance theory.

The contemporary relevance of WACC in an era of unprecedented change in financial markets, business models, and regulatory frameworks underscores both its enduring value and the need for continued innovation in its application. The challenges posed by ultra-low interest rates, the rise of alternative capital sources, the increasing importance of sustainability considerations, and the growing complexity of international business operations all require thoughtful adaptation of traditional WACC methodologies. These developments suggest that future applications of WACC may involve more sophisticated scenario analysis, dynamic adjustment mechanisms, and explicit consideration of factors that were peripheral to traditional calculations.

Looking forward, the democratisation of financial analysis through technological advancement promises to make sophisticated WACC calculations more accessible whilst potentially improving their accuracy through enhanced data availability and analytical capabilities. Artificial intelligence and machine learning applications may enable more nuanced risk assessment and more accurate beta estimation, whilst real-time market data feeds could support more dynamic and responsive cost of capital calculations. However, these technological enhancements will not eliminate the need for experienced judgement in interpreting results and adapting methodologies to specific circumstances.

The enduring importance of WACC in corporate finance reflects its unique ability to encapsulate complex market relationships and theoretical insights in a form that supports practical decision-making. As companies navigate an increasingly complex global business environment characterised by rapid technological change, evolving regulatory frameworks, and shifting investor preferences, the need for sophisticated approaches to cost of capital determination becomes ever more critical. WACC provides a conceptual anchor that enables decision-makers to evaluate opportunities systematically whilst remaining grounded in sound theoretical principles.

The comprehensive understanding of WACC developed through this analysis emphasises the importance of viewing the metric not as a mechanical calculation but as a framework for thinking systematically about the complex relationships between risk, return, and value creation in modern business enterprises. The theoretical foundations established by Modigliani and Miller, the practical refinements developed through decades of application, and the ongoing adaptations required by changing market conditions all contribute to a rich and evolving understanding of how companies can optimise their capital allocation decisions. In an era of unprecedented change and uncertainty, this systematic approach to cost of capital determination remains as relevant and valuable as ever, providing a stable foundation for navigating the complexities of modern corporate finance.

Quote: Henry Joseph-Grant - Just-Eat founder

“Ultimately an investment is an instrument of trust as much as it is of belief. Every single part of your strategy is showing you're accountable and understand your responsibility with that. Take ownership.” - Henry Joseph-Grant - Just-Eat founder

Henry Joseph-Grant is widely recognised as a leading figure in the tech entrepreneurship and investment space. His career exemplifies the journey from humble beginnings to achieving major influence across international markets. Raised in Northern Ireland, Joseph-Grant’s academic pursuit in Arabic at the University of Westminster equipped him for the global business landscape, notably in his advisory work in Dubai. He began working early—starting as a paperboy at 11 and moving into various sales roles, before a pivotal tenure with Virgin.

His operational calibre was cemented by his contribution to scaling JUST EAT from its UK startup phase to its landmark IPO, which resulted in a £5.25bn market capitalisation. He subsequently founded The Entertainer in partnership with Abraaj Capital, and has held senior leadership roles (Director, VP, C-level) at disruptive technology firms.

Henry’s perspective is shaped by deep, hands-on engagement: navigating companies through crises, managing dramatic operational turnarounds, and leading restructuring efforts during economic shocks such as the pandemic. His experience includes acting as an angel investor, mentoring CEOs (at Seedcamp, Pitch@Palace, PiLabs) and judging major entrepreneur competitions including Richard Branson’s VOOM Pitch to Rich. Recognised among the top 25 UK entrepreneurs by Smith & Williamson, Henry is committed to fostering new generations of innovators and business leaders.

Context of the Quote

The quote captures Joseph-Grant’s core philosophy: in both entrepreneurship and investment, trust is as fundamental as belief or analytical conviction. Strategy is not simply a matter of tactics; it is a public demonstration of accountability and stewardship for others’ capital—be that from shareholders, employees, or the wider community. Trust is built through transparent, consistent ownership of outcomes, both positive and negative. This philosophy became especially salient in his leadership during industry crises, where he led teams through abrupt, challenging change, instilling a culture of responsibility and resilience.

Relevant Theorists and Thought Leaders

Joseph-Grant’s worldview aligns with and extends a body of thinking on trust, accountability, and stewardship within investment and leadership circles:

• Peter L. Bernstein (1919-2009), author of "Against the Gods: The Remarkable Story of Risk", argued that all investment is a decision under uncertainty, underpinned by belief and the trustworthiness of those managing risk and capital. Bernstein traced the intellectual roots of taking and managing risk back to early insurance and probability theory, highlighting the psychological dimensions of trust inherent in capital allocation.

• Warren Buffett, considered the most successful investor of the modern era, has consistently emphasised the interplay between trust, character, and performance in capital deployment. His letters to Berkshire Hathaway shareholders stress that he seeks partners and managers who will act as if all company actions are subject to public scrutiny—a direct echo of Joseph-Grant’s call for ownership and accountability.

• Michael C. Jensen (emeritus professor, Harvard Business School) and William H. Meckling pioneered the concept of agency theory, which analyses the relationship between principals (investors) and agents (managers). Their analysis showed how trust and proper alignment of incentives are essential to guarding against opportunism and ensuring responsible stewardship.

• Charles Handy, the UK management thinker, championed the “trust economy”, where intangible trust stocks often surpass formal contracts in their influence over business outcomes. Handy’s reflections on responsibility-through-action parallel Joseph-Grant’s insistence that strategy is not just a plan, but an ongoing display of stewardship.

• Annette Mikes and Robert S. Kaplan (Harvard Business School) have explored risk leadership, demonstrating that trust is central to effective risk management; without authentic ownership from the top, frameworks fail.

Each of these theorists recognised that trust is not a soft attribute, but a measurable, actionable asset—and its absence carries material risk. Joseph-Grant’s phrasing highlights the imperative for every leader, founder, and investor: take ownership is not a cliché, but a competitive advantage and ethical responsibility.

Summary of Influence

The philosophy embedded in the quote is founded on Joseph-Grant’s lived experience, informed by crisis-tested leadership across markets and sectors. It reflects a broader intellectual tradition where trust, strategic clarity, and personal accountability are the cornerstones of sustainable investment and entrepreneurship. The challenge—and opportunity—posed is clear: in today’s interconnected, high-stakes environment, belief and trust are inseparable from value creation. Success follows when leaders are visibly accountable for the trust placed in them, at every level of the strategy.

Term: Internal Rate of Return (IRR)

The Internal Rate of Return (IRR) is a cornerstone metric in financial analysis, widely adopted in capital budgeting, private equity, real estate investment, and corporate strategy. IRR represents the annualised effective compounded return rate that will make the net present value (NPV) of all projected cash flows (both inflows and outflows) from an investment equal to zero. In essence, it is the discount rate at which the present value of projected cash inflows exactly balances the initial cash outlay and subsequent outflows.

Calculation and Application

IRR is derived using the following equation:

Where:

• C_t = net cash inflow for period t
• C_t = initial investment (outflow)
•  
• T = number of time periods

Analytical calculation of IRR is non-trivial (the formula is nonlinear in IRR), requiring iterative numerical methods or financial software to determine the rate that sets NPV to zero.

• IRR is expressed as a percentage and can be directly compared to a company’s cost of capital or required rate of return (RRR). An IRR exceeding these hurdles implies a financially attractive investment.
• IRR allows comparison across diverse investment opportunities and project types, using only projected cash flows and their timing. For instance, a higher IRR indicates a superior project, provided risks and other qualitative considerations are similar.

Role and Limitations

IRR incorporates the time value of money, recognising that early or larger cash flows enhance investment attractiveness. It is particularly suited to evaluating projects with well-defined, time-based cash flows, such as real estate developments, private equity funds, and corporate capital projects.

However, IRR also has notable limitations:

• If cash flows have complex sign changes, multiple IRRs can occur, complicating interpretation.
• IRR does not reflect scale — a small project may yield a high IRR but be insignificant in value.
• It assumes reinvestment of interim cash flows at the IRR, which may not be realistic in practice.
• IRR should be assessed alongside NPV, payback period, and scenario analysis to account for uncertainty in projections and limitations in model assumptions.

Strategic Context and Comparison

IRR is often used in conjunction with the Weighted Average Cost of Capital (WACC) and NPV in investment appraisal. While NPV provides the monetary value added, IRR offers a uniform rate metric useful for ranking projects.

Comparison to other measures:

• Compound Annual Growth Rate (CAGR): Unlike IRR, CAGR only considers start and end values, ignoring timing of intermediate flows.
• Return on Investment (ROI): ROI measures total percentage return but does not account for timing or annualisation as IRR does.

Key Takeaways

• IRR is the discount rate that equates the present value of future cash flows to the initial investment outlay (NPV = 0).
• It provides a basis for comparing investments and quantifying project attractiveness, especially when considering the timing and magnitude of returns.
• IRR should be interpreted within context, considering other financial metrics and qualitative factors.

Best Related Strategy Theorist: Irving Fisher

Irving Fisher (1867–1947) is most closely associated with the conceptual foundations underlying IRR through his pioneering work in the theory of interest and investment decision making.

Backstory: Fisher’s Relationship to IRR

Fisher, an American economist and professor at Yale University, fundamentally reconceptualised how investors and firms should evaluate projects and capital investments. In his seminal works — notably The Rate of Interest (1907) and The Theory of Interest (1930) — Fisher introduced the principle that the rate of return on an investment should be evaluated as the discount rate at which the present value of expected future cash flows equals the current outlay. This approach constitutes the essence of IRR.

Fisher’s "investment criterion" – now known as the Fisher Separation Theorem – provided a theoretical justification for corporate investment decisions being made independently of individual preferences, guided solely by maximisation of present value. His analytical frameworks directly inform the calculation and interpretation of IRR and paved the way for subsequent developments in capital budgeting and financial theory.

Biography

• • Academic Career: Fisher earned the first PhD in economics granted by Yale (1891), and remained a professor there throughout his life.
  • Intellectual Contributions:
    • • Developed the theory of interest and capital budgeting, introducing concepts foundational to IRR.
      • Pioneered the use of mathematical and statistical methods in economics.
      • Recognised for Fisher’s Equation, connecting inflation, real, and nominal interest rates; a precursor to numerous modern finance tools.
  • Influence: Fisher’s focus on discounting future cash flows and the time value of money made him a key figure not only in economics but also in finance. His ideas underpin many investment evaluation tools, including NPV and IRR, and have endured as best practice for investment professionals globally.

Fisher’s work bridges economic theory and practical strategy, making him the most authoritative figure associated with the conceptual foundations and strategic application of IRR.

Summary:

• IRR is the universal rate at which a project breaks even in NPV terms, holistically integrating the timing and magnitude of all cash flows.
• Irving Fisher’s theoretical developments directly underpin IRR’s use in modern financial strategy, establishing him as the most relevant strategy theorist for this concept.

Quote: Dan Borge - Creator of RAROC

“Risk management is designed expressly for decision makers—people who must decide what to do in uncertain situations where time is short and information is incomplete and who will experience real consequences from their decision.” - Dan Borge - Creator of RAROC

Backstory and context of the quote

• Decision-first philosophy: The quote distils a core tenet of modern risk practice—risk management exists to improve choices under uncertainty, not to produce retrospective explanations. It aligns with the practical aims of RAROC: give managers a single, risk-sensitive yardstick to compare opportunities quickly and allocate scarce capital where it will earn the highest risk-adjusted return, even when information is incomplete and time-constrained.
• From accounting profit to economic value: Borge’s work formalised the shift from accounting measures (ROA, ROE) to economic profit by adjusting returns for expected loss and using economic capital as the denominator. This embeds forecasts of loss distributions and tail risk in pricing, limits and capital allocation—tools designed to influence the next decision rather than explain the last outcome.
• Institutional impact: The RAROC system was explicitly built to serve two purposes—risk management and performance evaluation—so decision makers can price risk, set hurdle rates, and steer portfolios in real time, consistent with the quote’s emphasis on consequential, time-bound choices.

Who is Dan Borge?

• Role and contribution: Dan Borge is widely credited as the principal designer of RAROC at Bankers Trust in the late 1970s, where he rose to senior managing director and head of strategic planning. RAROC became the template for risk-sensitive capital allocation and performance measurement across global finance.
• Career arc: Before banking, Borge was an aerospace engineer at Boeing; he later earned a PhD in finance from Harvard Business School and spent roughly two decades at Bankers Trust before becoming an author and consultant focused on strategy and risk management.
• Publications and influence: Borge authored The Book of Risk, translating quantitative risk methods into practical guidance for executives, reflecting the same “decision-under-uncertainty” ethos captured in the quote. His approach influenced internal economic-capital frameworks and, indirectly, the adoption of risk-based metrics aligned with regulatory capital thinking.

How the quote connects to RAROC—and its contrast with RORAC

• RAROC in one line: A risk-based profitability framework that measures risk-adjusted return per unit of economic capital, giving a consistent basis to compare businesses with different risk profiles.
• Why it serves decision makers: By embedding expected loss and holding capital for unexpected loss (often VaR-based) in a single metric, RAROC supports rapid, like-for-like choices on pricing, capital allocation, and portfolio mix in uncertain conditions—the situation Borge describes.
• RORAC vs RAROC: RORAC focuses the risk adjustment on the denominator by using risk-adjusted/allocated capital, often aligned to capital adequacy constructs; RAROC adjusts both sides, making the numerator explicitly risk-adjusted as well. RORAC is frequently an intermediate step toward the fuller risk-adjusted lens of RAROC in practice.

Leading theorists related to the subject

• Dan Borge (application architect): Operationalised enterprise risk management via RAROC, integrating credit, market, and operational risk into a coherent capital-allocation and performance system used for both risk control and strategic decision-making.
• Robert C. Merton and colleagues (contingent claims and risk-pricing foundations): Option-pricing and intermediation theory underpinned the quantification of risk and the translation of uncertainty into capital and pricing inputs later embedded in frameworks like RAROC. Their work provided the theoretical basis to model loss distributions and capital buffers that RAROC operationalises for decisions.
• Banking risk-management canon (economic capital and performance): The RAROC literature emphasises economic capital as a buffer for unexpected losses across credit, market, and operational risks, typically calculated with VaR methods—central elements that make risk-adjusted performance comparable and actionable for management teams.

Why the quote endures

• It defines the purpose of the function: Risk is not eliminated; it is priced, prioritised, and steered. RAROC operationalises this by tying risk-taking to economic value creation and solvency through a single decision metric, so leaders can act decisively when the clock is running and information is imperfect.
• Cultural signal: Framing risk management as a partner to strategy—not a historian of variance—has shaped how banks, insurers, and asset managers set hurdle rates, rebalance portfolios, and justify capital allocation to stakeholders under robust, forward-looking logic.

Selected biographical highlights of Dan Borge

• Aerospace engineer at Boeing; PhD in finance (Harvard); ~20 years at Bankers Trust; senior managing director and head of strategic planning; architect of RAROC; later author and consultant on risk and strategy.
• The Book of Risk communicates rigorous methods in accessible language, consistent with his focus on aiding real-world decisions under uncertainty.
• Recognition as principal architect of the first enterprise risk-management system (RAROC) at Bankers Trust, with enduring influence on risk-adjusted measurement and capital allocation in global finance.

Term: Risk-Adjusted Return on Capital (RAROC)

RAROC is a risk-based profitability framework that measures the risk-adjusted return earned per unit of economic capital, enabling like-for-like performance assessment, pricing, and capital allocation across activities with different risk profiles. Formally, RAROC equals risk-adjusted return (often after-tax, net of expected losses and other risk adjustments) divided by economic capital, where economic capital is the buffer held against unexpected loss across credit, market, and operational risk, commonly linked to VaR-based internal models:

Risk-Adjusted Return on Capital (RAROC) measures the risk-adjusted return earned per unit of economic capital, enabling like-for-like performance assessment, pricing, and capital allocation across activities with different risk profiles.

Key components and calculation

• Numerator: risk-adjusted net income (e.g., expected revenues minus costs, taxes, expected losses, plus/minus transfer charges or return on risk capital), capturing the economic profit attributable to the position or business unit.
• Denominator: economic capital—the amount required to sustain solvency under adverse scenarios; it reflects unexpected loss and is often derived from portfolio risk models across credit, market, and operational risk.
• Decision rule: a unit creates value if its RAROC exceeds the cost of equity; this supports hurdle-rate setting and portfolio rebalancing.

What RAROC is used for

• Performance measurement: provides a consistent, risk-normalised basis to compare products, clients, and business lines with very different risk/return profiles.
• Capital allocation: guides allocation of scarce equity to activities with the highest risk-adjusted contribution, improving the bank’s economic capital structure.
• Pricing and limits: informs risk-based pricing, transfer pricing, and limit-setting by linking returns, expected loss, and required capital in one metric.
• Governance: integrates risk and finance by aligning business performance evaluation with the firm’s solvency objectives and risk appetite.

Contrast: RAROC vs RORAC

• Definition
  • RAROC: risk-adjusted return on (economic) capital; adjusts the numerator for risk (e.g., expected losses and other risk charges) and uses economic capital in the denominator.
  • RORAC: return on risk-adjusted capital; typically leaves the numerator closer to accounting net income minus expected losses, and focuses the adjustment on the denominator via allocated/risk-adjusted capital tied to capital adequacy principles (e.g., Basel).
   
• Practical distinction
  • RAROC is the more “fully” risk-adjusted metric—both sides are risk-aware, making it suited to enterprise-wide pricing, capital budgeting, and stress-informed planning.
  • RORAC is often an intermediate step that sharpens capital allocation by tailoring the denominator to risk, commonly used for business-unit benchmarking where the numerator is less extensively adjusted.
   
• Regulatory link
  • RORAC usage has increased where capital adjustments are anchored to Basel capital adequacy constructs; RAROC remains the canonical internal economic-capital lens for value creation per unit of unexpected loss capacity.

Best related strategy theorist: Dan Borge

• Relationship to RAROC: Dan Borge is credited as the principal designer of the RAROC framework at Bankers Trust in the late 1970s, which became the template for risk-sensitive capital allocation and performance measurement across global banks.
• Rationale for selection: Because RAROC operationalises strategy through risk-based capital allocation—prioritising growth where risk-adjusted value is highest—Borge’s work sits at the intersection of corporate strategy, risk, and finance, shaping how institutions set hurdle rates, manage portfolios, and compete on disciplined risk pricing.
• Biography (concise): Borge’s role at Bankers Trust involved building an enterprise system that quantified economic capital across credit, market, and operational risks and linked it to pricing and performance; this institutionalised the two purposes of RAROC—risk management and performance evaluation—in mainstream banking practice.

How to use RAROC well (practitioner notes)

• Ensure coherent risk adjustments: align expected loss estimates, transfer pricing, and diversification effects with the economic capital model to avoid double counting or gaps.
• Compare to cost of equity and peers: use RAROC-minus-cost-of-equity spread as the decision compass for growth, remediation, or exit; incorporate benchmark RAROC bands by segment.
• Tie to stress and planning: reconcile business-as-usual RAROC with stressed capital needs so that pricing and allocation remain resilient when conditions deteriorate.

Definitions at a glance

• RAROC = after-tax risk-adjusted net income ÷ economic capital.
• Economic capital = capital held against unexpected loss across risk types; often VaR-based internally, distinct from accounting equity and regulatory minimums.
• RORAC = (net income minus expected losses) ÷ risk-adjusted/allocated capital; commonly aligned to Basel-style capital attribution at business-unit level.

Quote: Dan Borge - Creator of RAROC

“The purpose of risk management is to improve the future, not to explain the past.” - Dan Borge - Creator of RAROC

This line captures the pivot from retrospective control to forward-looking decision advantage that defined the modern risk discipline in banking. According to published profiles, Dan Borge was the principal architect of the first enterprise risk-management system, RAROC (Risk-Adjusted Return on Capital), developed at Bankers Trust in the late 1970s, where he served as head of strategic planning and as a senior managing director before becoming an author and consultant on strategy and risk management. His applied philosophy—set out in his book The Book of Risk and decades of practice—is that risk tools exist to shape choices, allocate scarce capital, and set prices commensurate with uncertainty so that institutions create value across cycles rather than merely rationalise outcomes after the fact.

Backstory and context of the quote

• Strategic intent over post-mortems: The quote distils the idea that risk management’s primary job is to enable better ex-ante choices—pricing, capital allocation, underwriting standards, and limits—so future outcomes improve in expected value and resilience. This is the logic behind RAROC, which evaluates opportunities on a common, risk-sensitive basis so managers can redeploy capital to the highest risk-adjusted uses.
• From accounting results to economic reality: Borge’s work shifted emphasis from accounting profit to economic profit by introducing economic capital as the denominator for performance measurement and by adjusting returns for expected losses and unhedged risks. This allows performance evaluation and risk control to be integrated, so decisions are guided by forward-looking loss distributions rather than historical averages alone.
• Institutional memory, not rear-view bias: Post-event analysis still matters, but in Borge’s framework it feeds model calibration and capital standards whose purpose is improved next-round decisions—credit selection, concentration limits, market risk hedging—rather than backward justification. This is consistent with the RAROC system’s twin purposes: risk management and performance evaluation.
• Communication and culture: As an executive and later as an author, Borge emphasised that risk is a necessary input to value creation, not merely a hazard to be minimised. His public biographies highlight a practitioner’s pedigree—engineer at Boeing, PhD in finance, two decades at Bankers Trust—grounding the quote in a career spent building tools that make organisations more adaptive to future uncertainty.

Who is Dan Borge?

• Career: Aerospace engineer at Boeing; PhD in finance from Harvard Business School; 20 years at Bankers Trust rising to senior managing director and head of strategic planning; principal architect of RAROC; subsequently an author and advisor on strategy and risk.
• Publications: Author of The Book of Risk, which translates quantitative risk concepts for executives and general readers and reflects his conviction that rigorous risk thinking should inform everyday decisions and corporate strategy.
• Lasting impact: RAROC became a standard for risk-sensitive capital allocation and pricing in global banking and influenced later regulatory and internal-capital frameworks that rely on economic capital as a buffer against unexpected losses across credit, market, and operational risks.

How the quote connects to RAROC and RORAC

• RAROC (Risk-Adjusted Return on Capital): Measures risk-adjusted performance by comparing expected, risk-adjusted return to the economic capital required as a buffer against unexpected loss; it provides a consistent yardstick across businesses with different risk profiles. This enables management to take better future decisions on where to grow, how to price, and what to hedge—precisely the “improve the future” mandate.
• RORAC (Return on Risk-Adjusted Capital): Uses risk-adjusted or allocated capital in the denominator but typically leaves the numerator closer to reported net income; it is often a practical intermediate step toward the full risk-adjusted measurement of RAROC and is referenced increasingly in contexts aligned with Basel capital concepts.

Leading theorists related to the subject

• Fischer Black, Myron Scholes, and Robert Merton: Their option-pricing breakthroughs and contingent-claims insights underpinned modern market risk measurement and hedging, enabling the pricing of uncertainty that RAROC-style frameworks depend on to translate risk into required capital and pricing.
• William F. Sharpe: The capital asset pricing model (CAPM) provided a foundational lens for relating expected return to systematic risk, an intellectual precursor to enterprise approaches that compare returns per unit of risk across activities.
• Dan Borge: As principal designer of RAROC at Bankers Trust, he operationalised these theoretical advances into a bank-wide system for allocating economic capital and evaluating performance, embedding risk in everyday management decisions.

Why it matters today

• Enterprise decisions under uncertainty: The move from explaining past volatility to shaping future outcomes remains central to capital planning, stress testing, and strategic allocation. RAROC-style thinking continues to inform how institutions set hurdle rates, manage concentrations, and price products across credit, market, and operational risk domains.
• Cultural anchor: The quote serves as a reminder that risk functions add the most value when they are partners in strategy—designing choices that raise long-run risk-adjusted returns—rather than historians of failure. That ethos traces directly to Borge’s contribution: risk as a discipline for better choices ahead, not merely better stories behind.

Term: Return on Risk-Adjusted Capital (RORAC)

Return on Risk-Adjusted Capital (RORAC) is a financial performance metric that evaluates the profitability of a project, business unit, or company by relating net income to the amount of capital at risk, where that capital has been specifically adjusted to account for the risks inherent in the activity under review. It enables a direct comparison of returns between different business units, projects, or products that may carry differing risk profiles, allowing for a more precise assessment of economic value creation within risk management frameworks.

Formula for RORAC:

Return on Risk-Adjusted Capital (RORAC) evaluates the profitability of a project, business unit, or company by relating net income to the amount of capital at risk, where that capital has been specifically adjusted to account for the risks inherent in the activity under review.

Where risk-weighted assets are often synonymous with the capital allocated to cover potential unexpected losses – commonly referred to as economic capital, allocated risk capital, or even the regulatory value at risk. Unlike Return on Equity (ROE), which uses the company’s entire equity base, RORAC employs a denominator that adjusts for the riskiness of specific lines of business or transactions.

By allocating capital in proportion to risk, RORAC supports:

• Risk-based pricing at the granular (e.g. product or client) level
• Comparability across divisions with different risk exposures
• More effective performance measurement, especially in financial institutions where capital allocation is a critical management decision.

 

---

Contrast: RORAC vs. RAROC

 

Aspect	RORAC	RAROC
Acronym	Return on Risk-Adjusted Capital	Risk-Adjusted Return on Capital
Numerator	Net income (not risk-adjusted)	Net income (fully risk-adjusted; i.e., subtracts expected and unexpected losses)
Denominator	Risk-adjusted or allocated capital (economic/risk-weighted)	Same as RORAC: economic or risk-based capital
Main distinction	Only capital (denominator) is explicitly risk-adjusted	Both return (numerator) and capital (denominator) are fully risk-adjusted
Application	Evaluates how effectively risk-adjusted capital is being used to generate profit	Provides a total risk-based view; evaluates how much risk-adjusted profit is being earned per unit of risk-adjusted capital
Common use	Useful as an intermediate step between ROE and RAROC; supports capital allocation	Considered the “full step” in risk-sensitive performance management; benchmark for modern risk management systems
Origin/History	Appears as an evolution to make ROE more risk-aware	Developed at Bankers Trust in the 1970s by Dan Borge; widely adopted in banking

 

RORAC is a step beyond traditional metrics (like ROE) by recognising different risk profiles in how much capital is assigned, but does not fully risk-adjust the numerator. RAROC, by contrast, also incorporates provisions for expected losses and other direct adjustments to profitability, providing a purer view of economic value generation given all forms of risk.

---

Best Related Strategy Theorist: Dan Borge

Biography and Relevance:

Dan Borge is widely credited as the architect of RAROC, making him instrumental to both RAROC and, by extension, RORAC. In the late 1970s, while at Bankers Trust, Borge led a project to develop a more rigorous framework for risk management and capital allocation in banking. The resulting RAROC framework was revolutionary: it introduced a risk-sensitive approach to capital allocation, integrating credit risk, market risk, and operational risk into a unified model for measuring financial performance.

Borge’s contributions include:

• Establishing RAROC as a foundational risk management principle for global banks, influencing regulatory frameworks such as the Basel Accords.
• Advocating the principle that performance measurement should reflect not just raw returns but also the economic capital required as a buffer against potential losses.

Though Borge is not explicitly associated with RORAC by name, RORAC is widely recognised as an extension or adaptation of the principles he introduced – focusing especially on the risk-based allocation of capital for more effective resource deployment and incentive alignment.

Legacy in Strategy:
Dan Borge’s work laid the groundwork for risk-based performance management in financial institutions, making metrics such as RORAC and RAROC central to how banks, insurers, and investment firms manage risk and measure profitability today. His theories underpin much of contemporary capital allocation, risk pricing, and value-based management in these sectors.

---

Summary of Key Points:

• RORAC measures return based on risk-adjusted capital and is a bridge between ROE and fully risk-adjusted performance metrics like RAROC.
• RAROC adjusts both return and capital for risk, offering a more comprehensive risk/performance measure and forming the foundation of modern risk-sensitive management.
• Dan Borge is the most relevant theorist, having originated RAROC at Bankers Trust, and his legacy continues to influence the theory and application of RORAC.